Thanks Stephen Hawking for your wonderful contributions to humankind. When I was 14, you explained me the concepts of relativity and entropy with your book “A Brief History of Time” and it changed everything for me, especially the way I’ll understand Neurosciences and Brain-Computer Interfaces.
Who knows that several years later, I would work in a completely different field but with differential geometry and entropy concepts as a tool for, respectively, classifying my EEG data according to a natural metric corresponding to the mental states, and separating the hidden sources of the brain thanks to its link to independence ?
Today, I’m using those tools to classify electroencephalographic data in real time for Brain-Computer Interface systems, I’m analyzing specific sources of brain activity with really small signal-to-noise ratio and all of that in the context of social neurosciences. Thank you Stephen.
figure :
—-
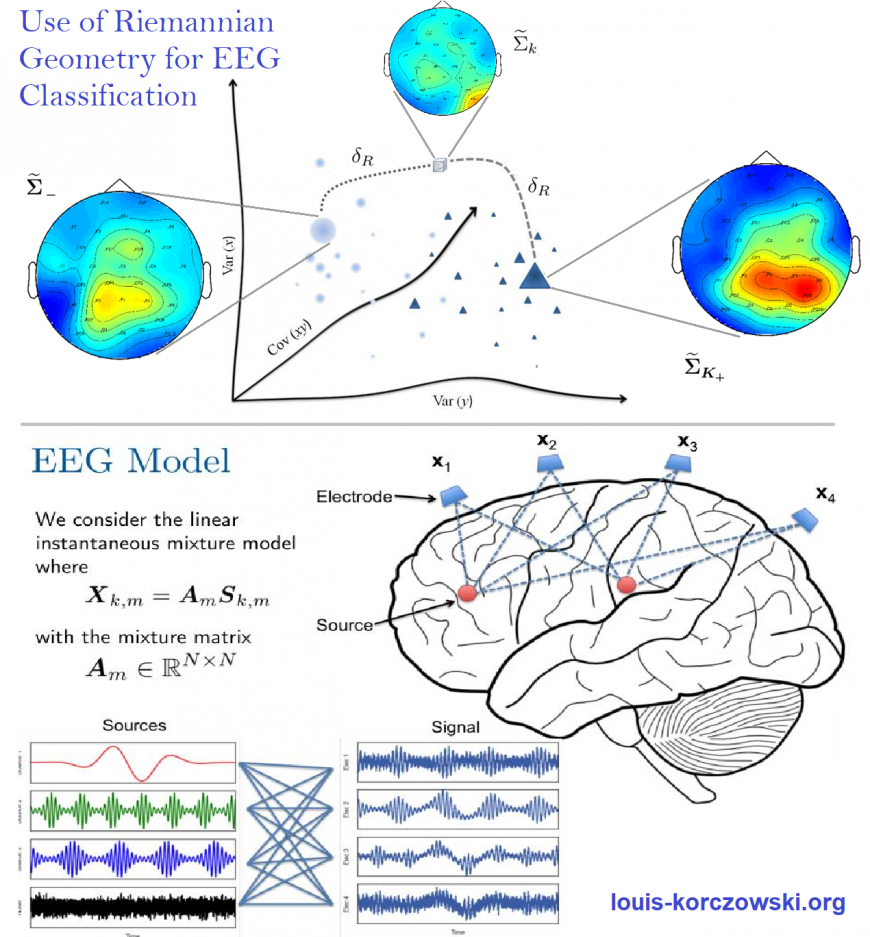
Top : All the second order statistics are encapsulated into the covariances matrices the EEG signal. Those covariances matrices are “living” in a manifold where their natural metric (distance, angles, etc.) are correct only locally.
One can use this natural metric (e.g. Fisher Information Metric) to define geometric means that can represent the stereotypical properties of one mental state (\Sigma_K+ or \Sigma_K-). Thus, when a new point appear (\Sigma_k), we can classify it according the geometric mean with respect to the metric.
—-
Bottom : The observations X recorded by non-invasive electrodes (EEG, in blue) are in fact a mixture of real neuronal sources S (in red).
One can find those hidden source by minimizing the mutual information (or maximizing the joint entropy), it is the principle of Blind Source Separation.